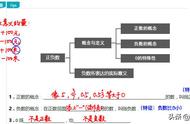
一、锐角三角函数
设RtABC的直角为C,三边分别为。
1.A的锐角三角函数
正弦:sinA=;
余弦:cosA=;
正切:tanA=.
2.特殊锐角的三角函数值
(1)sin30º=;sin45º=;sin60º=.
(2)cos30º=;cos45º=;cos60º=.
(3)tan30º=;tan45º=1;tan60º=.
3.锐角三角函数的取值范围
当A为锐角时,0<sinA<1,0<cosA<1,tanA>0.
4.锐角三角函数值的增减性
(1)锐角的正弦值随角度的增大(或减小)而增大(或减小);
(2)锐角的余弦值随角度的增大(或减小)而减小(或增大);
(3)锐角的正切值随角度增大(或减小)而增大(或减小).
5.三角函数值之间的关系
(1)若A B =90º,那么 sinA=cosB或sinB=cosA.
(2);.
二、解直角三角形及应用
1.解直角三角形的定义:由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形。
2.解直角三角形的依据
(1)三边之间的关系:.
(2)两锐角之间的关系:A B = 90º.
(3)边角之间的关系
<1>;
<2>;
<3>.
3.直角三角形的求解类型
(1)已知a,b:.
(2)已知a,c:.
(3)已知a,A:.
(4)已知a,B:.
(5)已知b,c:.
(6)已知b,A:.
(7)已知b,B:.
(8)已知c,A:.
(9)已知c,B:.
(10)已知A,B:a,b,c皆不可求。
4.解直角三角形的实际应用
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,选用适当的锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
,